COMBINING LIKE TERMS

Like terms are terms that have the literal coefficients, also known as a variable, the same. The numerical coefficient, that is the number on the left side of the literal coefficient, doesn't need to be the same. In short, having like terms always based on its literal coefficients. It is said to be collected, to simplify expressions in Algebra. Like terms includes powers and/or exponents. Constants also follow this rule but by simply adding or subtracting. Some short definition includes, like terms are terms in a series of Algebraic expression that has the same literal coefficients. Also, it is the similar literal coefficients, including power. The picture above was intentionally made colored to easily identify the like terms based on the letters and color. It should be noted that the algebraic term is separated by either 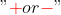$"{\color{Red} +}or{\color{Red} -}"$ , to be called a term.

Sample Step Guide on How to Do it

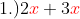
$1.) 2{\color{Red} x} +3{\color{Red} x}$ , the literal coefficients in this expression is "x". See that power is also 1. Thus 2x and 3x in this series of expressions are the same, that's why it is called "like terms". The numerical coefficients "2 and 3" need not be the same. To simplify, simply perform the given operation. We have addition, so to add 2x, and 3x gives us 5x, or 2x +3x =5x.

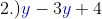
$2.) {\color{Blue} y}-3{\color{Blue} y}+4$ , in this series of expressions, the "y" is the common literal coefficients. There's 4 as a constant but since there are no other constants, we will leave it as is and copy at the end. So to simplify the expression, just perform the indicated operation. We have subtraction for expressions with literal coefficients on it, so by doing so, ${\color{Blue} y}-3{\color{Blue} y}=-2{\color{Blue} y}$ . 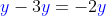Finally, we have -2y + 4, or to make it positive as first to write in the series, we have 4-2y.

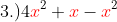
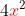
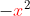
$3.) 4{\color{Red} x}^2+{\color{Red} x}-{\color{Red} x}^2$ , so this is a bit different from those previous examples. We have "x" as a common literal coefficient in this illustration. But notice that not all "x" has the same power. By definition, like terms include power or exponents to be the same. So in this case, we can only use the $4{\color{Red} x}^2$ and $-{\color{Red} x}^2$ , since these are the only terms that belong to the definition. To simplify them, we have $4{\color{Red} x}^2-{\color{Red} x}^2=3{\color{Red} x}^2$ . 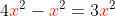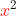So "x" and " ${\color{Red} x}^2$ " are said to be unlike terms. Meaning you cannot add nor subtract those.

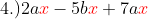
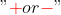
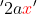
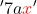
$4.) 2a{\color{Red} x}-5b{\color{Red} x}+7a{\color{Red} x}$ , here, all $"{\color{Red} x}"$ have the same power. But based on the previous definition that says " It should be noted that the algebraic term is separated by either $"{\color{Red} +}or{\color{Red} -}"$ , to be called a term", they have different compositions. We can say that only $'2a{\color{Red} x}'$ and $'7a{\color{Red} x}'$ have the same components with literal coefficients the same. 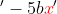The $'-5b{\color{Red} x}'$ is not included. 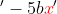So we cannot include $'-5b{\color{Red} x}'$ in simplifying the expression. Thus, $2a{\color{Red} x}-5b{\color{Red} x}+7a{\color{Red} x}=9a{\color{Red} x}-5b{\color{Red} x}$ . 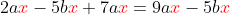This is how we can do so far for a simplified answer.

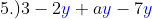
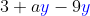
$5.) 3-2{\color{Blue} y}+a{\color{Blue} y}-7{\color{Blue} y}$ , this is almost the same as #4 example. We have "y" as common but "ay" is not. We have also "3" as a constant which is part of the expression but to deal as is. So to simplify, we have only $3+a{\color{Blue} y}-9{\color{Blue} y}$ . Some students attempt to simplify more because they thought that simplified answers don't look like two or more terms. But as long as no more terms to simplify, it would be final.

Example of Expression Problems with Easy Solutions

**State if the given is like terms or not (unlike terms), or partly.**

$1.) {\color{Red} x}{\color{Blue} y}^2+{\color{Red} x}^2{\color{Blue} y}=$ Click here!

$2.) {\color{Red} x}{\color{Blue} y}^2+{\color{Red} x}{\color{Blue} y^2}=$ Click here!

$3.) abc^2-bac^2 + c^2ba=$ Click here!

$4.) abc^2-2b^2ca + 3cba^2$ = Click here!

$5.) 2{\color{Red} x}^2{\color{Blue} y}z + 2{\color{Red} x}^2{\color{Blue} y}-2 {\color{Red} x}^2{\color{Blue} y} =$ Click here!

$6.) \frac{1}{2}ac+ \frac{2}{3}ac-\frac{3}{4}ac=$ Click here!

$7.) \frac{1}{4} b^3 c^2a + \frac{5}{2} a b^3 c^2$ = Click here!

$8.) \frac{1}{2}{\color{Red} x}{\color{Blue} y}^2 + \frac{1}{2} {\color{Red} x}^2{\color{Blue} y} - 2 {\color{Red} x}{\color{Blue} y}^2=$ Click here!

$9.) 3abc^2-b^2ca + cba2 =$ Click here!

$10.) mno + omn - nop =$ Click here!

Problems with Algebraic Equations and with Partial Solutions

Simplify the following if applicable. Some like terms were highlighted for easy spotting.

$1.)2xy-3xy-5 =$

$2{\color{Red} x}{\color{Blue} y}-3{\color{Red} x}{\color{Blue} y}-5 =$ Click here!

$2.)9-3{ x}^2{y}+5{x}^2{y}=$

$9-3{\color{Red} x}^2{\color{Blue} y}+5{\color{Red} x}^2{\color{Blue} y}=$ Click here!

$3.)\frac{2}{3}{x}{y}^2-\frac{2}{3}{x}{y}^2+\frac{4}{5}=$

$\frac{2}{3}{\color{Red} x}{\color{Blue} y}^2-\frac{2}{3}{\color{Red} x}{\color{Blue} y}^2+\frac{4}{5}=$ Click here!

$4.)3{a}c-4{a}bc+5ab=$

$3{{\color{Red} a}}{\color{Blue} b}c-4{{\color{Red} a}}{\color{Blue} b}c+5{\color{Red} a}{\color{Blue} b}=$ Click here!

$5.)2st-4+5st=$

$2{\color{Red} s}{\color{Blue} t}-4+5{\color{Red} s}{\color{Blue} t}=$ Click here!

$6.)2{s}^2 t}+5{s^3 t-5st=$

$2{\color{Red} s}^2{\color{Blue} t}+5{\color{Red} s}^3{\color{Blue} t}-5{\color{Red} s}{\color{Blue} t}=$ Click here!

$7.)\frac{3}{4}{a}+\frac{1}{4}{a}b-2{a}b=$

$\frac{3}{4}{{\color{Red} a}b}+\frac{1}{4}{{\color{Red} a}}b-2b=$ Click here!

$8.)2x^1y^2z^3-3xy^2z^3+4xyz=$

$2{\color{Red} x}^1{\color{Blue} y}^2{\color{DarkGreen} z}^3-3{\color{Red} x}{\color{Blue} y}^2{\color{DarkGreen} z}^3+4{\color{Red} x}{\color{Blue} y}{\color{DarkGreen} z}=$ Click here!

$9.)\frac{5}{6}mn+\frac{2}{6}mn-\frac{1}{3}mno=$

$\frac{5}{6}{\color{Red} m}{\color{Blue} n}+\frac{2}{6}{\color{Red} m}{\color{Blue} n}-\frac{1}{3}{\color{Red} m}{\color{Blue} n}{\color{DarkGreen} o}=$ Click here!

$10.){a}-{b}+{c}+2{b}=$