Word problem solving in Algebra: Distance Problem
Distance problem in Algebra is another type which involved time, and rates. Some students found this one not so easy, but some are good to deal with it, because the foundation of their preparation level seems not good. Apparently, Algebra is not every one's friend subject. Majority dislikes it. That's why this page was made.
In distance problem, we should consider the distance (d), time (t), and rate(r), Represented by the formula, , where d = distance, t =time, and r = rate. Variations were found below;
, where d = distance, t =time, and r = rate. Variations were found below;
If distance is unknown, use;
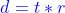
If time is unknown, use;
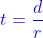
If rate is unknown, use;
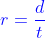
In the given formula above, we wanna find the unknown from the given problem and check what formula to use among the three. Usually, expect two moving vehicles, cars, trains, planes, etc., against each other and sometimes they go along together with one is faster.
Two trains traveling at the same direction. The slower train leaving the station and travels at the speed of 65 mph. After an hour, the fastest train leaves the same station at the speed of 75 mph. For how long a faster train over takes the slower?
Illustration:
So we need to make a table for us easy to figure out what is going on. The table below show the first set up as empty data .
In this case, we should start making up the data for two trains. We use "x" for the faster train time because this is the time by the slower train which will be added one hour to later meet the covered distance.
Note that "x" was in time (t) column and in a faster train row.
See the "x + 1" on the time (t) column and in a slower train row? The "1" indicates the time (one hour) elapsed to make their distance equal after the slower train leaves the station. So we can add their respective speeds now in the table, check the table below;
The 65 mph for slower train and 75 for the faster was set up respectively. Now let us work on their distances. Distance is found to be, d = r*t, so just multiply the time (t) and rate(r) from the tabular data. we're talking on "x + 1 and 65" for the slower and "x and 75" for the faster. So the table will now be completed by this look;
Did you see the gradual development of the data? From empty to filled up, it was now ready to do some Algebraic approach.
We need to equate their distance traveled. Knowing the distance they traveled was the same, so distance traveled by the slower train is equal to the distance traveled by the faster train, hence
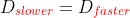
So,
65(x+1) = 75x, as working equation.
65x + 65=75x
65 = 75x - 65x
65 = 10x
x = 6.5, this means 6 hours and 30 minutes.
This is the speed required for the faster train to overtakes the slower train. Now for the question that "For how long a faster train over takes the slower?", we can tell it's 6 hours and 30 minutes,
This is so, because their time to met is unknown. So they both started at "x". See next progression;
So, to solve for what is asked;
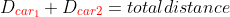
55x + 65x = 480
120x = 480
x = 4, this means 4 hours.
So after 4 hours,this is to answer the question "how long should these two cars meet?"
Example Problem 3
"Two cars leaving at the same point at exactly 8 in the morning. The blue car heading for west direction at 65 miles an hour. The red car going to east direction at 70 miles an hour. How long would they be 405 miles apart?"
Illustration:
Let's work on the equation;
65x + 70x = 405
x = 3. This means 3 hours after leaving at the same point at 8:00 in the morning.
So from 8:00 A.M. plus 3 hours, these two cars will be 405 miles apart at 11:00 in the morning, same day. This is to answer the question "How long would they be 405 miles apart?"
Solve this problem:
1. At Arizona, John drove from Kingman to Flagstaff at the speed of 65 mph. After one hour, his friend Josh traveled the same route at the speed of 80 mph. How long will Josh reach John given that they drive at their constant speed? Answer: 4 hours and 20 minutes
2. Jonathan, going to work, drove in a reservation at the speed of 55 mph, and increase his speed 20 mph the time he reaches Interstate Highway. He then roughly realize that he spent 10 minutes less time on Interstate Highway than on the reservation. If the distance from his house to work is 60 miles, find the total distance he traveled at the reservation assuming all his speed is constant. Answer: 54 minutes
3. A passenger train leave Los Angeles going to Arizona at 55 mph at 2:00 in the afternoon. At that exact time another train, a freight, from opposite direction travels at the speed of 65 mph going to Los Angeles. At what time these two trains meet accident? Answer: 5 pm
Click here to find your reference aid.
Talk to us
Distance problem in Algebra is another type which involved time, and rates. Some students found this one not so easy, but some are good to deal with it, because the foundation of their preparation level seems not good. Apparently, Algebra is not every one's friend subject. Majority dislikes it. That's why this page was made.
In distance problem, we should consider the distance (d), time (t), and rate(r), Represented by the formula,
If distance is unknown, use;
If time is unknown, use;
If rate is unknown, use;
In the given formula above, we wanna find the unknown from the given problem and check what formula to use among the three. Usually, expect two moving vehicles, cars, trains, planes, etc., against each other and sometimes they go along together with one is faster.
Example Problem 1
Two trains traveling at the same direction. The slower train leaving the station and travels at the speed of 65 mph. After an hour, the fastest train leaves the same station at the speed of 75 mph. For how long a faster train over takes the slower?
So we need to make a table for us easy to figure out what is going on. The table below show the first set up as empty data .
In this case, we should start making up the data for two trains. We use "x" for the faster train time because this is the time by the slower train which will be added one hour to later meet the covered distance.
Note that "x" was in time (t) column and in a faster train row.
See the "x + 1" on the time (t) column and in a slower train row? The "1" indicates the time (one hour) elapsed to make their distance equal after the slower train leaves the station. So we can add their respective speeds now in the table, check the table below;
The 65 mph for slower train and 75 for the faster was set up respectively. Now let us work on their distances. Distance is found to be, d = r*t, so just multiply the time (t) and rate(r) from the tabular data. we're talking on "x + 1 and 65" for the slower and "x and 75" for the faster. So the table will now be completed by this look;
Did you see the gradual development of the data? From empty to filled up, it was now ready to do some Algebraic approach.
We need to equate their distance traveled. Knowing the distance they traveled was the same, so distance traveled by the slower train is equal to the distance traveled by the faster train, hence
So,
65(x+1) = 75x, as working equation.
65x + 65=75x
65 = 75x - 65x
65 = 10x
x = 6.5, this means 6 hours and 30 minutes.
This is the speed required for the faster train to overtakes the slower train. Now for the question that "For how long a faster train over takes the slower?", we can tell it's 6 hours and 30 minutes,
Example Problem 2
"Two cars leaving from opposite direction. The first car travels to the right direction with the speed of 55 mph. At the same time, another car travels to the left direction at 65 mph. If the distance traveled by two cars from opposite direction is 480 miles, and given they maintain a constant speed, how long should these two cars meet?"
Illustration:
The topic on problem sample 1 is the train in the same direction. This is different, this is opposite in direction. So let's make a table to figure this out. See the table below;
So given their corresponding rate(speed).
Satisfying the formula for distance, d = r*t, Car from left is found by d=55x and from right is d=65x.
So, to solve for what is asked;
55x + 65x = 480
120x = 480
x = 4, this means 4 hours.
So after 4 hours,this is to answer the question "how long should these two cars meet?"
Example Problem 3
"Two cars leaving at the same point at exactly 8 in the morning. The blue car heading for west direction at 65 miles an hour. The red car going to east direction at 70 miles an hour. How long would they be 405 miles apart?"
Illustration:
So setting up the table for the Blue colored car, it show that;
Now, for both cars,
Let's work on the equation;
65x + 70x = 405
x = 3. This means 3 hours after leaving at the same point at 8:00 in the morning.
So from 8:00 A.M. plus 3 hours, these two cars will be 405 miles apart at 11:00 in the morning, same day. This is to answer the question "How long would they be 405 miles apart?"
Solve this problem:
1. At Arizona, John drove from Kingman to Flagstaff at the speed of 65 mph. After one hour, his friend Josh traveled the same route at the speed of 80 mph. How long will Josh reach John given that they drive at their constant speed? Answer: 4 hours and 20 minutes
2. Jonathan, going to work, drove in a reservation at the speed of 55 mph, and increase his speed 20 mph the time he reaches Interstate Highway. He then roughly realize that he spent 10 minutes less time on Interstate Highway than on the reservation. If the distance from his house to work is 60 miles, find the total distance he traveled at the reservation assuming all his speed is constant. Answer: 54 minutes
3. A passenger train leave Los Angeles going to Arizona at 55 mph at 2:00 in the afternoon. At that exact time another train, a freight, from opposite direction travels at the speed of 65 mph going to Los Angeles. At what time these two trains meet accident? Answer: 5 pm
Click here to find your reference aid.
Talk to us
























 Home
Home