Logical Statements and Quantifiers
This guide provides a structured approach to understanding logical statements and quantifiers, essential components in the study of logic and mathematics.
Why do we need to know about this?
Clear Thinking & Logic – Helps structure arguments precisely (e.g., "All rules apply to everyone" vs. "Some exceptions exist").
Math & Science Basics – Foundational for algebra, proofs, and laws (e.g., "Every action has an equal reaction").
Spotting Errors – Teaches how to disprove broad claims (e.g., "All politicians are corrupt" → Just one honest politician breaks this).
Real-Life Rules – Explains universal principles (e.g., "All passengers must show ID" means no exceptions).
In short: It sharpens reasoning skills for academics, debates, and everyday decision-making.
Logical statements and quantifiers are fundamental mathematics, computer science, philosophy, and linguistics tools. They help formalize arguments, construct proofs, define precise conditions, and reason about structures. Below are their key uses:1. Logical Statements (Propositions & Predicates)
Formalizing Arguments: Translating natural language statements into precise logical expressions (e.g., "If it rains, the ground gets wet" → R→WR→W).
Boolean Logic: Used in digital circuits, programming (if-else conditions), and truth tables.
Defining Conditions: Specifying rules in mathematics ("A number is even if it is divisible by;
2. Quantifiers (Universal ∀, Existential ∃)
A. Universal Quantifier (∀)
- States that a property holds for all elements in a domain.
- Example: ,("All real numbers have squares ≥ 0").
- Used in axioms (e.g., Peano arithmetic, set theory).
Take these 5 simple sentences explaining the Universal Quantifier (∀) with real-world examples
"All birds have wings.". Meaning: Every single bird, without exception, possesses wings.
"Every student in the class passed the exam.". Meaning: If you’re a student in that class, you passed—no one failed.
"Any triangle has three sides.". Meaning: Without exception, triangles (regardless of type) have 3 sides.
"All smartphones need electricity to work.". Meaning: If it’s a smartphone, it must have the power to function.
"Every citizen must obey the law.". Meaning: The rule applies to all citizens—no one is exempt.
- States that at least one element satisfies a property.
- Example:
("There exists a number whose square is 2"). - Used in proofs (e.g., constructive proofs, counterexamples).
Take these 5 simple sentences using the Existential Quantifier (∃) with real-world examples
"There exists a black swan.". Meaning: At least one swan in the world is black (though most are white).
- "Some students love mathematics.". Meaning: Not all, but at least one student enjoys math.
- "A triangle has three equal sides" (For equilateral triangles). Meaning: At least one type of triangle (equilateral) has equal sides.
- "There are smartphones that can fold.". Meaning: Not all, but some smartphones have folding screens.
- "Someone in this room has been to Paris.". Meaning: Among all people here, at least one has visited Paris.
Mathematical Proofs
Direct proofs, contradiction, and induction rely on quantified statements.
Example:
Computer Science
- Algorithm correctness (e.g., loop invariants use ∀).
- Database queries (SQL uses ∃ and ∀ implicitly).
Formal Logic & AI
- Knowledge representation (e.g., "All humans are mortal".
Linguistics & Philosophy
Analyzing meaning in language (e.g., "Every student passed" vs. "Some students passed").
Quantifier negation rules
¬∀xP(x)≡∃x¬P(x) ("Not all are P" ≡ "At least one is not P").
¬∃xP(x)≡∀x¬P(x) ("None exist" ≡ "All are not P").
Crucial in disproving statements (e.g., counterexamples).
Logical Statements
Definition. A logical statement is a declarative sentence that can be classified as either true or false, but not both.
Example:
"The sky is blue.""2 + 2 = 4."
"All cats are mammals."
Non-Examples:
"What time is it?" (Question)
"Close the door." (Command)
Understanding Quantifiers
1. General Truths
Statement: "All humans are mortal."
Logical Form: ∀x(Human(x)→Mortal(x))
Meaning: "For every x, if x is a human, then x is mortal."
2. Mathematics
Statement: "Every whole number added to zero remains the same."
Logical Form: ∀n(n+0=n)
Meaning: "For every number n, n+0 equals n."
3. Rules & Laws
Statement: "All passengers must wear seatbelts."
Logical Form: ∀ p (Passenger(p)→MustWearSeatbelt(p)
Meaning: "For every passenger p, p must wear a seatbelt."
4. Nature & Science
Statement: "All birds have feathers."
Logical Form: ∀b (Bird(b)→HasFeathers(b))
Counterexample: Penguins are birds but don’t fly, so this statement isn’t entirely true.
Original Statement: "All cats are black." (∀cBlack(c))
Negation Statement: "There exists at least one cat that is not black." (∃c ¬Black(c))
Key Takeaways
Universal quantifier (∀) = "For all" or "Every" → Makes a claim about every single item in a group.
Used in:
Science (laws of nature)
Math (rules like
Everyday rules ("All students must attend class.")
Negation: If "All X are Y" is false, then "At least one X is not Y."



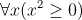












 Home
Home