LINEAR EQUATION
Linear equation In one Unknown
Linear equation in one unknown has the form 
as standard form where 
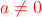and b are constants, and this is from the solution of equation 
.
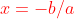Illustrative examples:
Solve for the value of unknown variable.
Literal equations:
Literal equations usually found in formulae. We usually solve for the values of each literal variable in the formula to know the required. Note that constant is a constant and need not to solve. Using Algebraic manipulations like what we did in the above mathematical manipulation, we can solve each unknown literals.
Illustrations:
Solve for r in the given equation.
Solution:
So we get the value of r literally.
Worded Problems:
Problem solving needs skill in Algebraic manipulations as tool to solve unknown variables. That is why in our previous work, notice that we were trained to do so. Problem solving needs steps to arrive the correct solution. The process is logical as it is its algorithm. In the first step, we need to translate the worded statement into a mathematical statement. Second is to find what is missing after writing the given. Third is to check the possibility of formula to use as approaches we have learned. And finally, to solve the problem.
Example 1:
The perimeter of a rectangle measures 60 feet and its length measures 10 feet more than its width. Find the dimensions of a rectangle.
Step 1(Given): Translation:
Perimeter p = 60 ft.
Length l = w+10 ft.
Width w = ?
Step 2 (Required): Missing is width
Step 3(Solution): Need the Formula to use
Solution:
Solving for w;
@ p = 60 ft and l = w +10 ft.
So the dimensions of the rectangle are the following:
Length = 20 ft.
Width = 10 ft.
Extra exercises:
1.) The sum of two numbers is 12 and their difference
is 7. What are the numbers?
2.) How
many liters of pure alcohol must be added to 12 liters of 60% alcohol solution
to get an 70% alcohol solution?
Write your answer in the "Post a comment" box found below this page. Let's see how you deal with it.
Click the link below for worksheet!!
Home
