Structure of linear programming are commonly of the form where two or more products involved. Example of these were mixtures of different ingredients like product 1(first ingredient), and product 2 (second ingredient). Each productions has its own machine as to manufacture but with limited time, say machine A can produce product 1 for a certain time and machine B for the second product with time limit as well. Each resulting product are subject to profit. We are expressing the idea that product 1 manufactured by machine A can be sell into x amount, and product 2 can be sell y amount. Linear Algebraic equation is needed to quantify each product. We must see to it that we are minimizing the material but maximizing the profit as programming intervention shows its importance, but still it depends on the case of the problem.
Where :
1.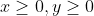 , this is so because we need to produce each product of x and/or y.
, this is so because we need to produce each product of x and/or y.
2.
 , this is restriction presented in inequalities.
, this is restriction presented in inequalities.
The presentation above was designed for two ingredients only. It can be more than two depending on how many ingredients were to be mixed. If ingredient 3 were added, it can be .
.
The objective here is to select from x and/or y that will be the objective function (aka profit function). The equation for the objective function was found by:
 , equation of objective function
, equation of objective function
There are some other ways to solve the linear programming problem. But the most fundamental and easiest one is the graphical method. This the most basic and convenient approach in solving such problem.
Take note also that our illustration not limits to two products, it can be three or more.
Let us have an illustration as example how to solve a simple problem involving Linear Programming.
Sample Problem:
How many units of x and y of the two compounds should be produced given the numbers of pounds for each of the ingredients based on the illustration below.
Illustrations:
Step 1: writing the given in-equations:
Ingredient 1:
Ingredient 2:
Step 2: Change the inequality symbol to equal symbol.
Now in order to graph these, we want to change the inequalities symbol into equal symbol.
Ingredient 1:
Ingredient 2:
Step 3: From ingredient A, set x=0 to get y, and y=0 to get x.This is to get the boundary as restrictions.
In equation 2x +3y=60,@x=0 y=20, and @ y=0 x=30. With this boundaries the graph were shown below.
Graph for 2x +3y=60.
And in equation x +2y=40,@x=0 y=20, and @ y=0 x=40.
Graph for x +2y =40.

Step 4: Graphing for its Feasible region
Illustration
Let two products be x and y. The set up for restrictions,profit, requirements were presented in tabular manner below. See photo provided.
Where :
1.
2.
The presentation above was designed for two ingredients only. It can be more than two depending on how many ingredients were to be mixed. If ingredient 3 were added, it can be
The objective here is to select from x and/or y that will be the objective function (aka profit function). The equation for the objective function was found by:
There are some other ways to solve the linear programming problem. But the most fundamental and easiest one is the graphical method. This the most basic and convenient approach in solving such problem.
Take note also that our illustration not limits to two products, it can be three or more.
Let us have an illustration as example how to solve a simple problem involving Linear Programming.
Sample Problem:
How many units of x and y of the two compounds should be produced given the numbers of pounds for each of the ingredients based on the illustration below.
Illustrations:
Step 1: writing the given in-equations:
Ingredient 1:
Ingredient 2:
Step 2: Change the inequality symbol to equal symbol.
Now in order to graph these, we want to change the inequalities symbol into equal symbol.
Ingredient 1:
Ingredient 2:
Step 3: From ingredient A, set x=0 to get y, and y=0 to get x.This is to get the boundary as restrictions.
In equation 2x +3y=60,@x=0 y=20, and @ y=0 x=30. With this boundaries the graph were shown below.
Graph for 2x +3y=60.
And in equation x +2y=40,@x=0 y=20, and @ y=0 x=40.
Graph for x +2y =40.

Step 4: Graphing for its Feasible region
The shaded yellow part was the feasible region.It is assumed that the students has back ground in inequalities shading.
Step 5: Solving for the objective function.(see from the table)
By solving for the value of x and y using substitution method, it was found by x=0 and y =20. Substituting these values to the objective function, we arrive to the following output;
















 Home
Home