MATRIX
Matrix or matrices is a rectangular array of numbers in the
form m x n where m is the row and n is the
column.
General Structures:
The amn stands for every location of a number in
the matrix. As an example a23 means 2
is at 2nd row and 3 at 3rd column. Note that the "vertical" formation of the matrix alignment is called column and row for "horizontal". Usually the upper case "a" is used in denoting matrix element and lower case "23 "for location of elements. Thus
More illustrations:
1.) The matrix
B = [ 2 1 4 -2 ], is 1 x 4 matrix since we have 1 row and 4 columns.
This is an example of 4x1 matrix.
B = [ 2 1 4 -2 ], is 1 x 4 matrix since we have 1 row and 4 columns.
2.) This matrix D,
is a 3 x 3 matrix since we have 3 rows and 3 columns.
3.) Matrix E below is an example of "3x2" matrix. It has three rows and two columns.
4.) Below is an example of Matrix with the size"5x1". Notice that we have five rows and one column.
5.) For the 4x5 size matrix, see below;
6.) Matrix I below is an example of Identity matrix.
We can add or subtract two matrices if and only if they are
equal in size, let’s say A=2 x 3, and B= 2 x 3. We can also multiply matrix of the same size provided that the
number of columns of the first matrix is equal to the number of row of the
second.
Illustration:
Notice that A has 3 x 3 matrix size and B has 3 x 3 matrix sizes. The red color in
the explanation tells that the two should be equal in order to qualify the operation.
So adding A and B;
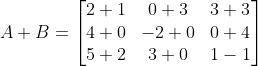
Answer
Subtracting B from A;
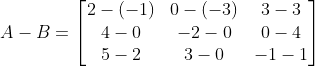
Answer
In the case of matrix C and D below,
and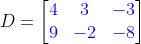 
We cannot perform the addition nor subtraction knowing that the size of each matrix is not qualified with each other. The matrix "C" has 3x2 and that of "D" was 2x3. We can only add or subtract from matrix to other matrix if both matrices are equal in size. But we can perform multiplication of matrices here. Observe the behavior of color patterns then, it was intentionally made to trace how they work.
So to multiply matrix C and D;
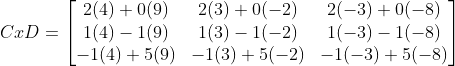
Answer
Note that the matrix D was written horizontally instead of original position.
Illustrative examples:
Given that:
, 
, 
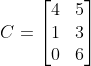
Compute for the following:
1.) A+B
2.) B+C
3.) B-A
4) BxC or B*C or BC (The product of B and C)
5.) AxB
Solution for # 1:
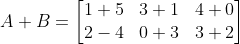
Answer
Solution for # 2: Not Applicable hence the matrices sizes not equal.
Solution for # 3:
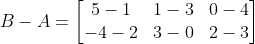
Answer
Solution for # 4:
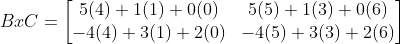
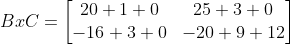
Answer
Solution for # 5: Not Applicable hence the matrices cannot be computed.
Extra exercises:
Given the matrices:
, 
, 
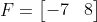
Compute for the following:
1.) D-E = ?
2.) ExF = ?
3.) E+D = ?
Show your final answer on the "Post a comment" box at the bottom of this page.
So adding A and B;
Subtracting B from A;
In the case of matrix C and D below,
We cannot perform the addition nor subtraction knowing that the size of each matrix is not qualified with each other. The matrix "C" has 3x2 and that of "D" was 2x3. We can only add or subtract from matrix to other matrix if both matrices are equal in size. But we can perform multiplication of matrices here. Observe the behavior of color patterns then, it was intentionally made to trace how they work.
So to multiply matrix C and D;
Note that the matrix D was written horizontally instead of original position.
Illustrative examples:
Given that:
Compute for the following:
1.) A+B
2.) B+C
3.) B-A
4) BxC or B*C or BC (The product of B and C)
5.) AxB
Solution for # 1:
Solution for # 2: Not Applicable hence the matrices sizes not equal.
Solution for # 3:
Solution for # 4:
Solution for # 5: Not Applicable hence the matrices cannot be computed.
Extra exercises:
Given the matrices:
Compute for the following:
1.) D-E = ?
2.) ExF = ?
3.) E+D = ?
Show your final answer on the "Post a comment" box at the bottom of this page.
Home
