solving inequalities by addition and subtraction

SOLVING INEQUALITIES BY ADDITION AND SUBTRACTION

Inequalities are statements of being unequal. The condition like 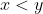$x<y$ is an illustration.

Inequalities has a property found below:

**If the same number is added to each side of a true inequality, the resulting inequality is also true.

Discussion:

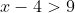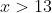Given the in-equation $x-4>9$ , to solve for the value of x, simply follow the Algebraic rule to apply like adding both sides by +4 to eliminate -4. In doing this we have $x-4{\color{Red} +4}>9{\color{Red} +4}$ . This would resulting to $x>13$ . If the in-equation having symbol looks like 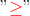$"{\color{Red} \geq }"$ , there's no changes in dealing with it by Algebraic expression. In the given in-equation 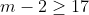$m-2\geq 17$ , solving for the value of m goes like $m-2{\color{Red} +2}\geq 17{\color{Red} +2}$ . And the result would be $m\geq 19$ . 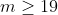In the in-equation $5x+7> 9+2x$ , we will be doing same approach to attack as the solution. We have $5x{\color{Red} -2x}+7{\color{Blue} -7}> 9{\color{Blue} -7}+2x{\color{Red} -2x}$ and make us the x>2/3 for the result. More illustration was provided below to gain more understanding.

More example for clarity.

1. In the in-equation $5+g\leq 3$ , the flow of the solution is;

$5+g\leq 3$ , Given in-equality

$5{\color{Red} -5}+g\leq 3{\color{Red} -5}$ , adding -5 to both sides to zero the left 5 on left member

${\color{Red} 0}+g\leq 3{\color{Red} -5}$ , now the result

${\color{Red} 0}+g\leq {\color{Red} -2}$ , now when 3-5 is computed

$g\leq {\color{Red} -2}$ , our final answer

2. In the in-equation 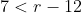$7<r-12$ , the flow of the solution is;

$7<r-12$ , Given in-equality

$7{\color{Red} +12}<r-12{\color{Red} +12}$ , adding +12 to both sides to zero the right -12 on right member

$19<r-0$ ,when 7+12 was computed on the left and -12+12 on the right is computed

$19<r$ , the result as final answer or can be written as;

$r>19$ , answer

More Illustrations:

Solve each given inequality.

$1.)y-4<3$

$y-4{\color{Red} +4}<3{\color{Red} +4}$

${\color{Blue} y<7}$

$2.) 2x+5>7$

$2x+5{\color{Red} -5}>7{\color{Red} -5}$

$2x>2$

$\frac{1}{2}*2x>2*\frac{1}{2}$

${\color{Blue} x>1}$

$3.) 3>8+r$

$3{\color{Red} -8}>8{\color{Red} -8}+r$

$-5>r$ , or can be written as

${\color{Blue} r<-5}$

$4.) -5\geq 11+d$

$-5{\color{Red} -11}\geq 11{\color{Red} -11}+d$

$-16\geq d$ , or can be written as

${\color{Blue} d\leq -16}$

$5.) 3x+5\geq 2x$

$3x+5{\color{Red} -5}\geq 2x{\color{Red} -5}$

$3x\geq 2x{\color{Red} -5}$

$3x{\color{DarkGreen} -2x}\geq 2x{\color{DarkGreen} -2x}{\color{Red} -5}$

$3x{\color{DarkGreen} -2x}\geq -5$

${\color{Blue} x\geq -5}$

$6.) 2a\leq -4+a$

$2a{\color{DarkGreen} -a}\leq -4+a{\color{DarkGreen} -a}$

${\color{Blue} a\leq -4}$

$7.) -3\geq p-5$

$-3{\color{Red} +5}\geq p-5{\color{Red} +5}$

$2\geq p$ , or can be written as

$p\leq 2$

In numbers 8-10,Define a variable and write the inequality and solve for it.

8.) The sum of a number and 4 is at least 8.

$x+4\geq 8$

$x\geq 4$

9.) A number decreased by 8 is less than 10.

$x-8<10$

$x<18$

10.) Twice a number is more than the sum of that number and 11.

$2x>x+11$

$x>11$

Extra exercises:

Mentally, solve for the value of defined variable. Write your answer on a "Post a comment" box found below of this page.

Solve for the value of x.

$1.) x+3<5$

$2.) 3x+y\geq <5x+3$

3.) The sum of twice a number and 7 is at most 4 less than the number.

DMG

solving inequalities by addition and subtraction

Posted by : Allan_Dell on Wednesday, March 14, 2018 | 4:46 PM