Algebraic Functions: First Derivative
An equation that has only a single answer for the "y" in every "x", is a function. Function has only one output as a result to every input in the equation, y = x, or, y = f(x)= x. Some symbols simplified written as f(x), g(x), h(x), etc. The given f(x) = x+ 2, when f(1) is asked for the function, it means that, we wanna find the function when "x" is at 1.
In differential calculus, we find their derivatives. We use "y' " for f '(x), "y' read as 'y prime' or y first derivative", or sometimes , we found them with their first derivative as;
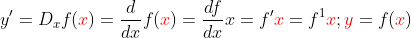
We knew that in differential calculus, we have the following rules of derivatives like;
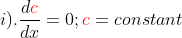
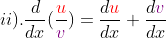
 ; (u and v are function of x)
; (u and v are function of x)
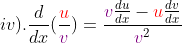
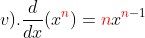
Now, see our illustrative examples.
Illustrative Examples
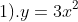
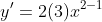
 , ans
, ans
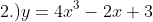
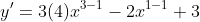
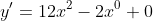
 , ans
, ans
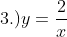
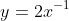
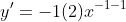
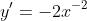
 , ans
, ans
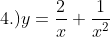
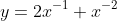
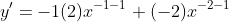
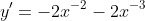
 , ans
, ans
Sample Problems with solution:
Differentiate the following Algebraic Functions.
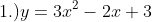
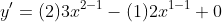
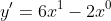
 , ans
, ans
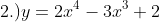
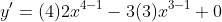
 , ans
, ans
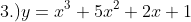
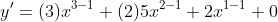
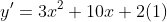
 , ans
, ans
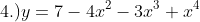
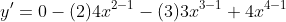
 , ans
, ans
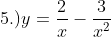
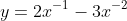
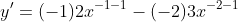
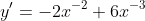
 , ans
, ans
Pop Quiz:
Differentiate the following, with partial solution:
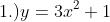
 , partial solution
, partial solution
 click here to write your final answer
click here to write your final answer
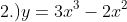
 , partial solution
, partial solution
 click here to write your final answer
click here to write your final answer
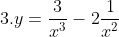
 , partial solution
, partial solution
 click here to write your final answer
click here to write your final answer
TAKE A SHORT QUIZ:
Differentiate the following Algebraic Functions. (YouTube solution soon)
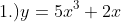
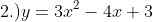
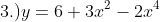
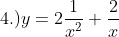
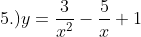
More exercises on derivative:
If you see typographical or any error(s), please feel free "Post a comment" below.
An equation that has only a single answer for the "y" in every "x", is a function. Function has only one output as a result to every input in the equation, y = x, or, y = f(x)= x. Some symbols simplified written as f(x), g(x), h(x), etc. The given f(x) = x+ 2, when f(1) is asked for the function, it means that, we wanna find the function when "x" is at 1.
In differential calculus, we find their derivatives. We use "y' " for f '(x), "y' read as 'y prime' or y first derivative", or sometimes , we found them with their first derivative as;
We knew that in differential calculus, we have the following rules of derivatives like;
Now, see our illustrative examples.
Illustrative Examples
Sample Problems with solution:
Differentiate the following Algebraic Functions.
Pop Quiz:
Differentiate the following, with partial solution:
TAKE A SHORT QUIZ:
Differentiate the following Algebraic Functions. (YouTube solution soon)
More exercises on derivative:
If you see typographical or any error(s), please feel free "Post a comment" below.
Join us in:
Tumblr
Internal References: link 1, link 2 , link 3
External References: link 1, link 2, link 3











 Home
Home
+ comments + 1 comments
Is this Algebra or Calculus