DOMAIN AND RANGE IN MATHEMATICS

DOMAIN AND RANGE

Each function is a relation in which each element in the domain is paired with exactly one element of the range.

  
By literal definition, the domain is all the "x" values in the form of "(x,y)" you can see in an ordered pair, while the range is all "y" values in the form of "(x,y)" in an ordered pair. A set of ordered pairs is called "relation". A relation can be a form of a specified rule, an equation, a tabular presentation, etc. The first set of components in the set of ordered pairs is called the domain and the second set of components is called range. As an example of a set of ordered pairs (1,4),(2,4),(2,5),(3,6), 1,2,2,3 all in red color is our domain and 4,4,5,6 in blue is our range.

Function. A relation is a function if and only if each element in the domain is paired by exactly one element of the range. This literally means that the domain or the "x" in the set of 
 "(x,y)" should appear once. In the example of ordered pairs (1,4),(2,4),(2,5),(3,6), "2" appears twice and this disqualifies the relation to be a function.

Note!: "All functions are relations, but not all relations are functions."

Illustration:

·      1.  Given the set of ordered pairs, state the domain, the range, and identify if it is a "function" or "not a function".

           The ordered pair : (1, 4), (2, 4), (2, 5), (3, 6).

Illustration:

Answer:

1.) The Domain: (1, 2, 2, 3), "By practical and literal identification, Notice that "2" appear twice". The element should appear no more than one to qualify for a function. Hence the relation is "Not a function"

2.) The Range: (4, 4, 5, 3). "By practical and literal identification, any range can appear more than one"

3.) This relation is "not a function". By definition, a relation is a function if and only if each element in the domain is paired by exactly one element of the range. In the illustration above, 
"2 was paired by 4 and 5". It is "not clear" what is the real partner (pair) of 2, is it really 4 or 5?" Which is which?

·         2.  From the given ordered pair, determine if the given set is a function or relation, and state the domain and the range.
         
            The ordered pair : (1, 4), (2, 5), (3, 6), (7, 4).

Illustration:

Answer:

1.) The domain: (1,2,3,7). "By practical and literal identification, Notice that all elements appear once". The element should appear no more than one to qualify for a function. Hence the relation is "A function"

2.) The range: (4,5,6,4)

3.) This relation is "a function". By definition, a relation is a function if and only if each element in the domain is paired by exactly one element of the range. In the illustration above, 
all domains were paired by a unique range. It is "clear" what is the real partner of each domain.

3.) Given the relations, Identify, which relations are functions.

a) (2,3), (3,8), (4,5), (5,7)

b) (1,4), (2,6), (1,5), (3,5)

c) (4,3), (4,6), (4,4), (5,9)

Answer:

a) (2,3), (3,8), (4,5), (5,7) -Function

b) (1,4), (2,6), (1,5), (3,5) -Not

c) (4,3), (3,6), (4,4), (5,9) -Not

       Can you tell why the other two were not a function? If so, briefly explain or discuss your answer in the "Post a comment" box found below this page.

4). Find the domain and range of the given equation,  .

  In equation form, notice that there are x and y in  . All real numbers are the domain here since we can put any number we want to have the values for "y". Check the process below.

In the equation ,

 @ x = 0,    

        

        y = 1

Hence, (0,1)

@ x = 1,    

        

        y = 2

Hence, (1,2)

@ x = 2,    

        

        y = 5

Hence, (2,5)

@ x = -1,    

        

        y = 2

Hence, (-1,2)

@ x = -2,    

        

        y = 5

Hence, (-2,5)

So the set of ordered pairs are: {(0,1),(1,2),(2,5), (-1,2),(-2,5)}.

Domain:{0,1,2,-1,-2}

Range:{1,2,5,2,5}

Practically, did you see the domain appeared twice or more? If no, then the equation is a function.

5.) Given the equations below, which of these equations where y is a function of x?

Answers:

Following the process on example #4,

 - Function

 - Function

 - Function

 - Not a function

     Can you tell why the last equation 3d is "not a function"? If so, briefly explain or discuss your answer on the "Post your comment" found below this page.

Extra exercises:

In the given equation below, what number is "not" a function? Tell us your answer by clicking here!









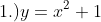
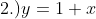
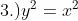
Check the link below for worksheets:

PDF worksheet with key

References:

DOMAIN AND RANGE

Talk to us on Pinterest, Facebook, Twitter, Instagram, Tumblr.

Check our Select button to Share at the bottom for more services!

Post your comments here!