What is an Axiom?

What is an Axiom?

Axiom - a statement or statements assumed to be true without proof, which a system was made. It is the building block that makes everything else work. It is a starting point of the logical flow of a system. It is an order. Axioms usually told as also a postulate. But axiom is more in general than postulate which is more specific. Axioms cannot be both true and false at the same time.

Further, nn axiom is a statement or proposition that is assumed to be true without needing proof or demonstration. Axioms serve as the foundation for a system of reasoning or a theory, and are used to derive other statements or conclusions through logical deduction.

In mathematics, axioms are also known as postulates, and are used to define the basic properties and relationships of mathematical objects, such as numbers, points, lines, and planes. For example, Euclid's postulates are a set of axioms that form the basis for Euclidean geometry.

In philosophy, axioms are used to establish basic principles or truths that are taken to be self-evident or intuitively obvious. These axioms may form the basis for a particular ethical or moral system, or for a system of metaphysics or epistemology.

The term "axiom" can also be used more broadly to refer to any fundamental principle or assumption that underlies a particular field of knowledge or inquiry.

Examples:

1.) The world is round.

2.) We are all humans.

3.) Integers are whole numbers.

4.) We need air to breathe.

5.) All triangles have three sides.

6.) The whole is greater than the sum of its parts.

 

7.) A straight line segment can be drawn joining any two points.

 

8.) For every action, there is an equal and opposite reaction. 

 

9.)All men are mortal.

 

10.)The shortest distance between two points is a straight line.

 

11.) All right angles are equal.

 

12.)Every number is either even or odd.

 

13. )Parallel lines never meet.

 

14.)The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides.

 

15.) If A equals B, and B equals C, then A equals C."Anything that is universally true and accepted is an axiom".

Some  Mathematical Axioms

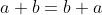
 , commutative law of addition

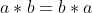
,  commutative law of multiplication

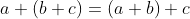
, associative law of addition

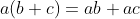
, distributive property over addition

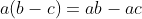
 , distributive property over subtraction

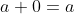
 , additive identity property

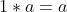
 , multiplicative identity property

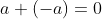
 , additive inverse property
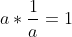
 ,  multiplicative inverse property

 
 

More Mathematical Axioms with Samples.

 

1.) The reflexive property of equality: For any number a, a = a. 

 

For example: 5 = 5.

 

2.) The transitive property of equality: If a = b and b = c, then a = c. 

For example: if x + y = 10 and y - z = 5, then x + (y - z) = 10 - 5, and so x + y - z = 5, which implies that x + y = z + 5.

 

3.) The commutative property of addition: For any numbers a and b, a + b = b + a. 

For example: 3 + 5 = 5 + 3. 

 

4.) The associative property of multiplication: For any numbers a, b, and c, (a x b) x c = a x (b x c). 

For example: (2 x 3) x 4 = 6 x 4 = 24, and 2 x (3 x 4) = 2 x 12 = 24.

 

5.) The distributive property of multiplication over addition: For any numbers a, b, and c, a x (b + c) = (a x b) + (a x c). 

For example: 2 x (3 + 4) = 2 x 3 + 2 x 4 = 6 + 8 = 14. 

6.) The axiom of induction: If a statement is true for the first natural number (usually 1), and if the statement is true for any natural number n, then the statement is also true for n + 1. 

For example: the statement "1 + 2 + ... + n = n x (n+1) / 2" is true for n = 1, and if it is true for some value of n, then it is also true for n + 1.

 

7.) The commutative property of multiplication: For any numbers a and b, a x b = b x a. 

For example: 2 x 3 = 3 x 2. 

 

8.) The associative property of addition: For any numbers a, b, and c, (a + b) + c = a + (b + c). 

For example: (1 + 2) + 3 = 1 + (2 + 3) = 6. 

 

9.) The identity property of multiplication: For any number a, a x 1 = a. 

For example: 5 x 1 = 5.  

 

10.) The identity property of addition: For any number a, a + 0 = a. 

For example: 8 + 0 = 8.

 

The seven (7) Euclid Axioms

1. Things which are equal to the same thing are equal to one another.

 
2. If equals are added to equals, the wholes are equal.

 
3. If equals are subtracted from equals, then the remainders are equal.

 
4. Things which coincide with one another are equal to one another.

 
5. The whole is greater than the part.

 
6. Things which are double of the same things are equal to one another.

 
7. Things that are halves of the same things are equal to one another.

Can you add anything that is universally accepted as an axiom? Then, share it with us by clicking here!

Or talk to us on Facebook, Twitter, Instagram, Pinterest, Tumblr.

Post your comment here!

Check our Select button to Share at the bottom for more services!