OPERATIONS WITH REAL NUMBERS
 |
| Click photo source |
Operations with real numbers in algebra refer to the basic arithmetic operations that can be performed on real numbers, which include addition, subtraction, multiplication, and division. Real numbers are numbers that can be represented on the number line, including both rational and irrational numbers.
Here is a brief explanation of each operation:
Addition: Adding two or more real numbers together produces a sum that is also a real number. For example, 3 + 4 = 7, and -2.5 + 1.3 + 0.7 = -0.5.
Subtraction: Subtracting one real number from another produces a difference that is also a real number.
For example, 7 - 4 = 3, and -2.5 - 1.3 = -3.8.
Multiplication: Multiplying two or more real numbers together produces a product that is also a real number.
For example, 3 x 4 = 12, and -2.5 x 1.3 x 0.7 = -2.275.
Division: Dividing one real number by another produces a quotient that is also a real number, unless the divisor is zero.
For example, 12 / 4 = 3, and -2.275 / 1.3 = -1.75.
These operations can be used to manipulate and solve equations involving real numbers.
Rational Numbers:
A rational number is a number that can be expressed as the ratio of two integers, where the denominator is not equal to zero. In other words, a rational number is any number that can be written in the form p/q, where p and q are integers and q is not equal to zero.
For example, 1/2, -3/4, 5/6, and 0 are all rational numbers. However, π (pi) and √2 (square root of 2) are not rational numbers, because they cannot be expressed as the ratio of two integers.
Rational numbers can be positive, negative, or zero. They can also be expressed in decimal form, either as a terminating decimal (such as 0.5 or -0.75) or a repeating decimal (such as 0.333... or -1.6).
Irrational Numbers:
An irrational number is a number that cannot be expressed as the ratio of two integers. In other words, an irrational number is any number that cannot be written in the form p/q, where p and q are integers and q is not equal to zero.
Irrational numbers are numbers that have non-repeating, non-terminating decimal expansions. For example, the number π (pi) is an irrational number, and its decimal expansion continues indefinitely without repeating a pattern. Other examples of irrational numbers include the square root of 2, the square root of 3, and the golden ratio.
It is important to note that the set of irrational numbers is infinite and uncountable, which means that there are more irrational numbers than there are rational numbers.
Operations On Real Numbers:
Example: Perform the following operations:
(5 + 3) x (4 - 2)
Solution:
First, we need to simplify the expression inside the parentheses:
5 + 3 = 8 (Adding 5 and 3) 4 - 2 = 2 (Subtracting 2 from 4)
Now we have:
(8) x (2)
Next, we can perform the multiplication:
8 x 2 = 16
Therefore, the final answer is 16.
In this example, we are given an expression that involves addition and multiplication of real numbers. The expression consists of two pairs of parentheses that contain real numbers. We need to perform the addition and subtraction operations first, and then multiply the results together.
We start by evaluating the expression inside the first set of parentheses. We add 5 and 3 to get 8, and we subtract 2 from 4 to get 2. We replace the expressions inside the parentheses with their results:
(5 + 3) x (4 - 2) = 8 x 2
Next, we perform the multiplication operation by multiplying 8 and 2 to get the final answer of 16.
Rational:
Example: Perform the following operations:
Solution:
First, we need to find a common denominator for the fractions inside the parentheses. The smallest common multiple of 3 and 4 is 12. We can convert the fractions 2/3 and 1/4 to have a denominator of 12:
2/3 = 8/12 (Multiplying the numerator and denominator by 4) 1/4 = 3/12 (Multiplying the numerator and denominator by 3)
Now we have:
Next, we can perform the addition inside the first set of parentheses:
We replace the expression inside the parentheses with the result:
Finally, we can perform the multiplication:
Therefore, the final answer is
In this example, we are given an expression that involves addition and multiplication of rational numbers. The expression consists of two pairs of parentheses that contain fractions. We need to find a common denominator for the fractions inside the parentheses, perform the addition operation, and then multiply the results together.
We start by finding the smallest common multiple of the denominators of the fractions inside the parentheses, which is 12. We convert the fractions 2/3 and 1/4 to have a denominator of 12 by multiplying their numerators and denominators by 4 and 3, respectively. This gives us the fractions 8/12 and 3/12, which we can add together:
We replace the expression inside the first set of parentheses with the result of the addition, and then perform the multiplication of the two fractions:
The expression (2/3 + 1/4) x (5/6) simplifies to 55/72 by finding a common denominator, performing the addition operation, and then performing the multiplication operation.
Irrational:
Example: Perform the following operations:
Solution:
First, we need to find an approximate value for each irrational number.
The square root of 2 is approximately 1.41421356. The square root of 3 is approximately 1.73205081.
Now we can add the approximations together:
1.41421356 + 1.73205081 = 3.14626437
Therefore, the approximate value of
In this example, we are given an expression that involves addition of irrational numbers. The expression consists of two square roots that cannot be simplified to a rational number. We need to find an approximate value for each irrational number, and then add them together.
Finding an exact value for irrational numbers can be difficult, so we often use approximations to perform operations on them. In this case, we found the approximate values for the square roots of 2 and 3 by using a calculator or by using a method such as the Babylonian method.
Once we have the approximations, we can simply add them together to get an approximation for the sum of the two irrational numbers. In this example, we added the approximations for √2 and √3 to get an approximate value of 3.14626437 for their sum.
The expression √2 + √3 has an approximate value of 3.14626437, which was found by finding approximate values for each irrational number and then adding them together.
Identification:
Identify if the given is rational or irrational numbers.
- 0.5 =
- √2 =
- 2/5 =
- -2 =
- π =
- 3/4 =
- e =
- √7 =
- 1.333... =
- φ
Sample Problems
Problem 1:
Find the value of x that satisfies the equation below.
Solution:
We can start by cross-multiplying to get rid of the fractions:
Expanding the left side and simplifying (by distributing 2 and 5 respectively), we get:
Subtracting 8x from both sides:
14 = 2x - 15
Adding 15 to both sides:
29 = 2x
Dividing by 2:
x = 29/2
Therefore, the solution to the equation is x = 29/2, which is a rational number.
The Straight Process:
Problem 1:
Find the value of x that satisfies the equation below.
Solution:
14 = 2x - 15
29 = 2x , or finally
x = 29/2 , Answer
_______________________________________________________________________
Problem 2:
Solve for the value of x:
Solution:
We start by cross-multiplying to eliminate the denominator:
,eliminating the reds
Distributing 3 on the right terms:
2x + 1 = 3x - 9
Bringing all the terms to one side, we get:
2x - 3x = -9 - 1
Simplifying, we get:
-x = -10
Dividing both sides by -1, we get:
x = 10
Therefore, the solution is x = 10.
The Straight Process:
Solve for the value of x:
Solution:
,
2x + 1 = 3x-9
2x - 3x = -9 - 1
-x = -10
x = 10 , Answer
______________________________________________________________________
Problem 3:
Solve for the value of x:
Solution:
We start by cross-multiplying to eliminate the denominators:
Expanding both sides gives us:
Bringing all the terms to one side, we get:
Using the quadratic formula:
where:
a = 7
b = -14
c = 1
Simplifying:
Therefore, the solutions are:
and
The Straight Process:
Solve for the value of x:
Solution:
Using the quadratic formula:
where:
a = 7
b = -14
c = 1
Therefore, the solutions are:
and
______________________________________________________________________
Problem 4:
Solve for the value of x:
Given that,
Solution:
First, cross-multiply to eliminate the fractions:
Cancel out expressions in red.
Multiply both sides by 2, to eliminate denominator 2.
Cancel out the reds, we get,
.
Simplify and solve for x:
4x + 10 = 3x - 9, so
x = -19 , Answer
The Straight Process:
Solve for the value of x:
Given that,
Solution:
.
4x + 10 = 3x - 9, so

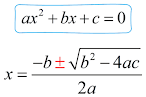









 Home
Home