What are Polynomials?

Click for Photo Credit

Where:
- is the polynomial function.
- is the variable.
- is a non-negative integer called the degree of the polynomial.
- are constants called coefficients.
Now, let's look at some illustrations of different types of polynomials:
Constant Polynomial:
.This is a degree 0 polynomial and represents a horizontal line at .
Linear Polynomial:
.This is a degree 1 polynomial, representing a straight line with a slope of 3 and a y-intercept at 2.
Quadratic Polynomial:
This is a degree 2 polynomial, representing a parabola that opens upwards with its vertex at (2, 0).
Cubic Polynomial:
. This is a degree 3 polynomial, representing a cubic curve with varying concavity.
- Quartic Polynomial:. This is a degree 4 polynomial, which can have complex curves with multiple turning points.
Polynomials are incredibly important in mathematics and various fields due to their versatile and powerful nature. Here are some reasons why polynomials hold such significance:
Function Approximation: Polynomials can approximate a wide range of functions, which makes them valuable for simplifying complex functions and calculations. This is particularly useful in engineering, physics, and computer graphics.
Equation Solving: Polynomials often appear in equations that need to be solved for specific values. The solutions of polynomial equations provide critical insights into various problems, ranging from physics equations to financial models.
Curve Fitting: Polynomial functions can be used to fit curves to sets of data points. This is crucial in statistics, data analysis, and scientific research for extracting trends and patterns from experimental data.
Root Finding: Finding the roots (solutions) of polynomial equations is a fundamental mathematical problem. Techniques like the Newton-Raphson method rely on polynomials to approximate solutions iteratively.
Optimization: Many optimization problems involve finding the maximum or minimum of a polynomial function. These problems arise in economics, engineering design, and operations research.
Computer Graphics: Polynomial functions play a significant role in computer graphics for modeling curves, surfaces, and animations. Bézier curves and surfaces, used extensively in graphics, are based on polynomial equations.
Control Systems: Polynomials are used in control theory to design and analyze dynamic systems, such as in robotics, aerospace engineering, and industrial automation.
Signal Processing: Polynomials are used in digital signal processing for tasks like filtering, noise reduction, and signal analysis.
Cryptography: Polynomials have applications in cryptography, where they are used to create encryption and decryption algorithms that rely on the properties of polynomial operations.
Numerical Methods: Polynomials are often used in numerical methods for solving differential equations, integration, and differentiation, forming the basis for many computational techniques.
Algebraic Geometry: Polynomials are central to algebraic geometry, a field that studies the geometry of solutions to polynomial equations. This has connections to various areas of mathematics and even theoretical physics.
Mathematical Modeling: Polynomials offer a versatile tool for constructing mathematical models of real-world phenomena, enabling scientists and researchers to describe and predict various processes.
Here are a few simple problems on polynomials with solutions.
Problem 1:
Find the value of
Solution :
Substitute into the polynomial:
Problem 2:
Factor the polynomial,
Solution :
To factor the quadratic polynomial, we look for two numbers whose product is the constant term () and whose sum is the coefficient of the linear term (). Those numbers are and , so we can factor as:
Problem 3:
Simplify the expression
Solution :
Combine like terms (terms with the same exponent):
Problem 4:
Find the roots of the quadratic equation below.
Solution :
This quadratic equation can be factored as
which means the only solution is .Problem 5:
Given that,
Solution:
Add the two polynomials term by term:
More Exercises
Problem 1:
Find the degree of the polynomial .
Solution:
The highest power of is 4.
Answer: The degree is 4.
Problem 2:
Add the polynomials and
Solution:
Answer: .
Problem 3:
Multiply
Solution:
Use the distributive property:
.
Answer: .
Problem 4:
Factor the polynomial .
Solution:
Find two numbers that multiply to 6 and add to -5:
.
Answer:
Problem 5:
Solve for : .
Solution:
Factor the equation:
or .
Answer: or .




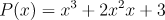






















 Home
Home