FACTORING QUADRATIC EQUATION
 |
| Standard Form of Quadratic Equation |
Above is the standard form of the quadratic equation. The power "2" in "x" as the variable is the indicator that the equation is in the second order thus quadratic. The letters, in color, are the numerical coefficient and constant (c = 5). Being basic in quadratic, let us be reminded that the equation involves both "+" and "-" to separate the term. A term is an Algebraic expression, not an equation. There are like and unlike terms in an equation. Below are the simple illustrations of like and unlike terms.
The
quadratic equation is a mathematical formula that is used to solve quadratic
equations of the form ax^2 + bx + c = 0, where a, b, and c are constants. The
quadratic equation has a wide range of uses in various fields of study,
including:
1.
Solving problems in physics and engineering: The quadratic
equation is used to solve problems in physics and engineering that involve
motion, acceleration, velocity, and distance. For example, the quadratic
equation can be used to determine the trajectory of a projectile, the maximum
height reached by a ball thrown into the air, or the time it takes for a car to
come to a stop.
2.
Analyzing financial data: The quadratic equation is used in
financial analysis to model and analyze data related to investments, interest
rates, and financial forecasting. For example, the quadratic equation can be
used to calculate the yield on a bond, the break-even point for a business, or
the optimal price for a product.
3.
Solving geometric problems: The quadratic equation is used in
geometry to solve problems related to areas, volumes, and distances. For
example, the quadratic equation can be used to find the area of a circle, the
volume of a cylinder, or the distance between two points in three-dimensional
space.
4.
Solving optimization problems: The quadratic equation is used in
optimization problems to find the maximum or minimum value of a function. For example,
the quadratic equation can be used to find the maximum or minimum value of a
parabolic arch, the optimal location for a satellite, or the best design for a
bridge.
Overall, the quadratic equation is a powerful mathematical tool that has a wide range of uses in various fields of study. Its versatility and applicability make it an essential formula for anyone interested in solving problems related to motion, finance, geometry, and optimization.
Like Terms:
Unlike Terms:
 |
Just to remind you to focus on the term. It is separated by "+" and "-" signs. If one of them is mismatched with the other except the numerical then it is said it is an unlike term.
The FOIL Method in Factoring Quadratic Equation.
This is one way to familiarize the process of factoring quadratic equations, the FOIL method. Based on the picture above, the sequence was applied, e.i. First-Outside-Inside-Last for the sequence. Just go to this site for more explanation.
Illustrations:
Problem 2:
A quadratic equation is given by: x^2 + 4x - 5 = 0
To solve this equation, we can use the quadratic formula, which
is:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
In this equation, a, b, and c are the coefficients of the
quadratic equation ax^2 + bx + c = 0.
Using the quadratic formula, we can find the roots of the
quadratic equation:
x = (-4 ± sqrt(4^2 - 4(1)(-5))) / 2(1)
Simplifying this expression, we get:
x = (-4 ± sqrt(44)) / 2
x = (-4 ± 2sqrt(11)) / 2
x = -2 ± sqrt(11)
Therefore, the solutions to the quadratic equation x^2 + 4x - 5
= 0 are:
x = -2 + sqrt(11) or x = -2 - sqrt(11)



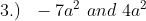





































 Home
Home